DeepDiff 5 is finally here!
Delta Object
The Delta object is introduced.
DeepDiff Delta is a directed delta that when applied to t1 can yield t2 where delta is the difference between t1 and t2.
The Delta objects are like git commits but for structured data.
You can convert the diff results into Delta objects, store the deltas, and later apply to other objects.
Example:
>>> t1 = [1, 2, [3, 5, 6]]
>>> t2 = [2, 3, [3, 6, 8]]
>>> diff = DeepDiff(t1, t2, ignore_order=True, report_repetition=True)
>>> diff
{'values_changed': {'root[0]': {'new_value': 3, 'old_value': 1}, 'root[2][1]': {'new_value': 8, 'old_value': 5}}}
>>> delta = Delta(diff)
>>> delta
<Delta: {'values_changed': {'root[0]': {'new_value': 3}, 'root[2][1]': {'new_value': 8}}}>
>>> t1 + delta == t2
True
Note that we can apply delta to objects different than the original objects they were made from:
>>> t3 = ["a", 2, [3, "b", "c"]]
>>> t3 + delta
[3, 2, [3, 8, 'c']]
And it comes with Numpy support:
>>> from deepdiff import DeepDiff, Delta
>>> import numpy as np
>>> t1 = np.array([1, 2, 3, 5])
>>> t2 = np.array([2, 2, 7, 5])
>>> diff = DeepDiff(t1, t2)
>>> delta = Delta(diff)
>>> delta + t1
array([2, 2, 7, 5])
>>> delta + t2 == t2
array([ True, True, True, True])
There is way more to Delta from serialization for storing Delta to other details.
Read more about Delta object here.
Deep Distance
The concept of Deep Distance is introduced.
Deep Distance is the distance between 2 objects. It is a floating point number between 0 and 1. Deep Distance in concept is inspired by Levenshtein Edit Distance.
At its core, the Deep Distance is the number of operations needed to convert one object to the other divided by the sum of the sizes of the 2 objects capped at 1. Note that unlike Levensthtein Distance, the Deep Distance is based on the number of operations and NOT the “minimum” number of operations to convert one object to the other. The number is highly dependent on the granularity of the diff results. And the granularity is controlled by the parameters passed to DeepDiff.
>>> from deepdiff import DeepDiff
>>> DeepDiff(10.0, 10.1, get_deep_distance=True)
{'values_changed': {'root': {'new_value': 10.1, 'old_value': 10.0}}, 'deep_distance': 0.0014925373134328302}
>>> DeepDiff(10.0, 100.1, get_deep_distance=True)
{'values_changed': {'root': {'new_value': 100.1, 'old_value': 10.0}}, 'deep_distance': 0.24550408719346048}
>>> DeepDiff(10.0, 1000.1, get_deep_distance=True)
{'values_changed': {'root': {'new_value': 1000.1, 'old_value': 10.0}}, 'deep_distance': 0.29405999405999406}
>>> DeepDiff([1], [1], get_deep_distance=True)
{}
>>> DeepDiff([1], [1, 2], get_deep_distance=True)
{'iterable_item_added': {'root[1]': 2}, 'deep_distance': 0.2}
>>> DeepDiff([1], [1, 2, 3], get_deep_distance=True)
{'iterable_item_added': {'root[1]': 2, 'root[2]': 3}, 'deep_distance': 0.3333333333333333}
>>> DeepDiff([[2, 1]], [[1, 2, 3]], ignore_order=True, get_deep_distance=True)
{'iterable_item_added': {'root[0][2]': 3}, 'deep_distance': 0.1111111111111111}
Read more about Deep Distance here.
Improved granularity of results when ignore_order=True
>>> from pprint import pprint
>>> from deepdiff import DeepDiff
>>> t1 = [
... {
... 'key3': [[[[[1, 2, 4, 5]]]]],
... 'key4': [7, 8],
... },
... {
... 'key5': 'val5',
... 'key6': 'val6',
... },
... ]
>>>
>>> t2 = [
... {
... 'key5': 'CHANGE',
... 'key6': 'val6',
... },
... {
... 'key3': [[[[[1, 3, 5, 4]]]]],
... 'key4': [7, 8],
... },
... ]
In DeepDiff 4:
>>> pprint(DeepDiff(t1, t2, ignore_order=True))
{'iterable_item_added': {'root[0]': {'key5': 'CHANGE', 'key6': 'val6'},
'root[1]': {'key3': [[[[[1, 3, 5, 4]]]]],
'key4': [7, 8]}},
'iterable_item_removed': {'root[0]': {'key3': [[[[[1, 2, 4, 5]]]]],
'key4': [7, 8]},
'root[1]': {'key5': 'val5', 'key6': 'val6'}}}
In DeepDiff 5:
>>> pprint(DeepDiff(t1, t2, ignore_order=True, cache_size=5000, cutoff_intersection_for_pairs=1))
{'values_changed': {"root[0]['key3'][0][0][0][0][1]": {'new_value': 3,
'old_value': 2},
"root[1]['key5']": {'new_value': 'CHANGE',
'old_value': 'val5'}}}
Pretty print
Use the pretty method for human readable output regardless of what view you have used to generate the results.
>>> from deepdiff import DeepDiff
>>> t1={1,2,4}
>>> t2={2,3}
>>> print(DeepDiff(t1, t2).pretty())
Item root[3] added to set.
Item root[4] removed from set.
Item root[1] removed from set.
New Optimizations
Many new optimizations are introduced, especially when dealing with nested data structures, numeric lists and, Numpy arrays.
Read about optimizations here.
Caching
Caching can dramatically improve the performance for nested objects especially when ignore_order=True.
For example, lets take a look at the performance of the benchmark_deeply_nested_a in the DeepDiff-Benchmark repo.
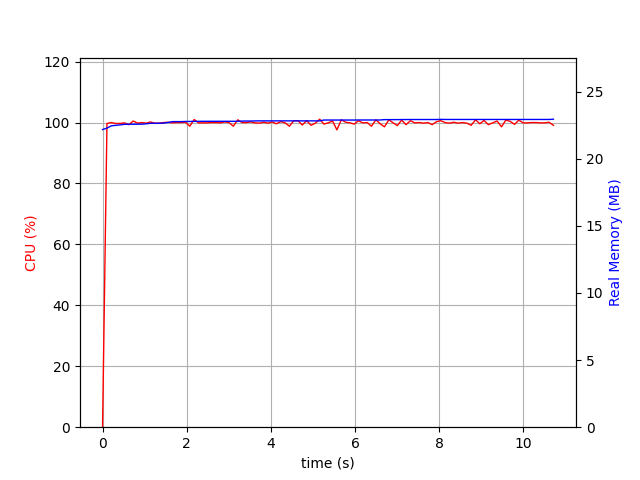
Without any caching it takes 10 seconds to do the diff!
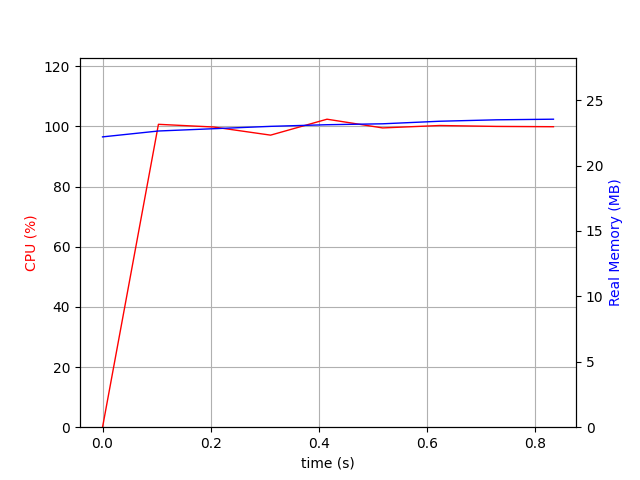
And with caching it takes under a second:
Improved Numpy Support
Previously, DeepDiff barely supported Numpy. DeepDiff 5 comes with a much more comprehensive support of Numpy.
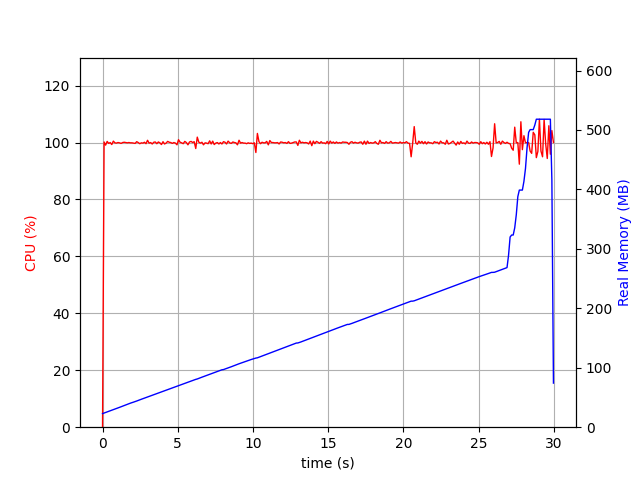
For example, a sample diff with numbers took up to 30 seconds without the optimizations:
And 5 seconds with Numpy optimizations:
Read more about optimizations here.
Conclusion
DeepDiff 5 comes with many new features and improvements. Please star it on github if you find it useful.
I would like to thank everybody who helped this release possible from creating PR’s, to beta testings, and providing feedback.